Working with Arrays and Matrices
By default, the dimensions of the display grid are set to a single cell. Many people regularly use the calculator without ever being aware that it can support matrices, or more generally, arrays of numbers. And many fields of problems probably do not require this feature. But if you need to do matrix or vector arithmetic, solve sets of simultaneous equations, work with complex numbers, convert between co-ordinate systems, you will need to use this powerful feature. Please note that if you are using a handheld computer with a version of WindowsCE prior to 3.0 (generally the older devices) the matrix functions will not be available.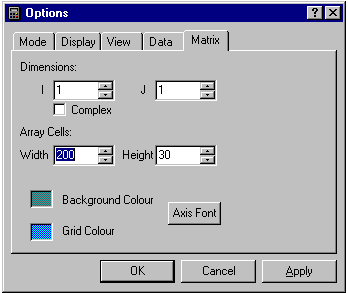
The dimensions of the display grid can be set using the Matrix tab of the Options dialog. When the dimensions are greater than 1x1, additional functions become available as described below when the shift button is depressed. Some functions are dependent on certain restrictions on dimensions for them to be available. If the I dimension is set to exactly two, you can check the "Complex" box to use complex numbers.
It may be necessary to enlarge the display by changing the size of the
calculator window in order to see the grid of values. On WindowsCE
(e.g. Pocket PC) you will not be able to enlarge the whole calculator,
but you can make more display area available by reducing the size of the
buttons, and possibly discarding the fifth row of function buttons.
You may also need to experiment with the font sizes for both the buttons
and the display. You can also reduce the level of precision to make
it possible to use narrower columns. Once you have selected array mode,
the display in some ways resembles a spreadsheet program such as Excel.
Displaying Arrays and Matrices
When using arrays of numbers (see the section on the Mode dialog tab), the display is divided into a number of array cells on a grid. The colour of this grid is set by the bottom of the three colour wells.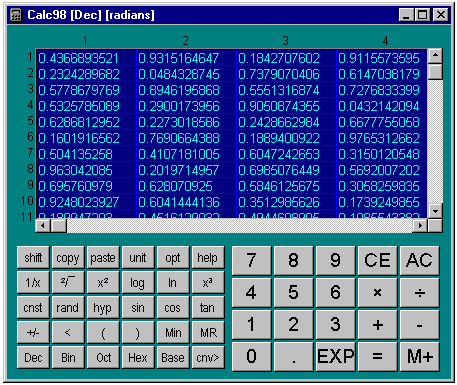
The dimensions (in pixels) of each grid cell is defined by the Array Cells Width and Height edit boxes.
The axes are drawn using the font specified using the Font dialog obtained by pressing the Axis Font button. The axis background is set using the middle of the three colour wells.
Simple arithmetic with arrays
When you first enter array mode you will see that all the array cells are selected and that if you do a simple calculation it will be simply repeated in each cell. This is how simple array arithmetic works, applying each operation to all of the cells, and clearly this alone is not particularly useful. But in array mode a number of buttons have new or enhanced functions. For example, pressing the "rand" button now produces an array of random numbers (make sure you are in decimal mode).In the examples below we assume you are using algebraic logic. If you are using RPN you need to enter the values onto the stack and use the post entry operators in the normal way.
 - Index
- Index
If you click the shift button the "rand" button becomes "ind", which gives
each cell the value of its own index. Now we can do something mildly
useful: select decimal, degree mode and make the array size 10 x 9. Click
on "ind" (SHIFT + rand). Click "+" then "1"
(notice how all cells are filled with 1). Click "=". All cells now
have the value of their own index plus one, i.e. values from 1 to 90. Now
click the "sin" button and you have an instant table of the sines
of whole degree angles. If the results look odd, check that you remembered
to set the angle mode to degrees.
Let's suppose you want to repeat this operation with other trigonometric functions, square root, etc., but you don't want to have to compute the index + 1 every time. Simply save the intermediate result to memory using the "Min" button. All the memories work in array mode, (although only the value of the first array element is visible in the dialog when selecting the memory).
Selecting cells and ranges of cells
Initially, all the cells are selected, but you can also select an individual cell by clicking on it with the mouse or with the stylus on a WindowsCE device. When you select a cell, the remaining cells are dimmed. It feels quite natural to use the stylus in this way. You can also select a rectangular group of cells by pressing the left mouse button on one cell and releasing it after moving to another (on pen computers you press the stylus on a cell and move the stylus across the display surface and then release from another cell). Alternatively you can select a single cell and then SHIFT+select another cell to indicate a range of cells. You can scroll the display before the second of these operations, making it possible to select a range of cells even if it is not possible to view them all on the display at the same time.Finally, you can use the keyboard (or virtual keyboard) cursor control keys (arrow keys) to move the selection around. This works in any mode except the "Time" mode, when the arrow keys control the stopwatch. The HOME and END keys on the keyboard will select the very first or last cells of the grid. If a range of cells are selected, the whole range moves around the grid as you use the cursor keys. The "next" button on the main keypad can also be used to advance a single cell at a time. The keyboard INSERT (or INS) key does the same thing. This is useful if you want to enter all the values in a matrix in turn.
You can select all the cells by clicking outside the grid if the display area is larger than the grid, or using one of the techniques above. If the grid is too big for the display you will get scroll bars to move the grid and the area outside the grid will not be visible, but there is a small button where the two scroll bars meet which can be used to select all the cells. There is also a "Select All" option in the Edit menu. Clicking on "AC" also selects all cells as well as deleting the contents.
Once you have selected a single cell or a group of cells, all subsequent
arithmetic operations act on those cells only. Selecting an individual
cell allows you to make complete calculations on that one cell alone.
You can then move to another cell or include it in a larger group of cells
and do further calculations. Example: you want a table of numbers
and their square roots up to 10. First set the array dimensions to 2 x
11. Select all the cells in the first column and click on "ind"
(shift "rand"). Select the second column and index it in the
same way. With the second column still selected click on the square
root button.
Using copy and paste
The copy button (or Ctrl-C on the keyboard) can be used to copy the contents of the selected cell or cells into the clipboard. You can then select a single cell and use the paste button (or Ctrl-V on the keyboard) to copy the data back starting at the location of the cell. If the dimensions of the group of cells copied is too large for the array size specified the extra data is discarded. If you make a selection of a group of cells and then use paste, only the selected cells are updated from the clipboard, even if the clipboard data contains a larger selection. If the clipboard data contains a smaller group of cells than the selection the cells beyond the range of the clipboard data are left unchanged.Copying data to the clipboard also makes the data available to other applications such as a word processor or spreadsheet. The same process can be used in reverse to import data from other applications. Example: using the example above, make sure all the cells are selected and click on the copy button. Run a spreadsheet program such as Excel (or Pocket Excel on a handheld device), select a cell and select Paste from the Edit menu. The data are now pasted into the worksheet and can be further processed, printed or incorporated into another spreadsheet. You can do the same process in reverse, copying data to the clipboard within another application and then pasting it into the array in the calculator.
You can use cut and paste within the calculator application as a convenient
way of copying or moving blocks of data within an array, or storing for
a later calculation. Because the clipboard only allows you to store
one set of data at a time, you may need to make use of the memories for
more complex calculations. You should also bear in mind that data
is saved to the clipboard as text in whatever display format is currently
selected. This means that if you are only using a small number of
decimal places there could be a loss of precision compared with, say, using
the memory. It also means that if you store data in the clipboard
in, hexadecimal mode, for example, and then switch to decimal mode, the
clipboard will still contain data in hexadecimal which will be interpreted
as decimal. This will probably not give the desired result.
Matrix arithmetic
Matrix arithmetic has special rules. Matrix addition and subtraction are conveniently defined as the sum or difference of the individual elements and this is the same as the simple array arithmetic operation described above, which therefore needs no further work on our part.Example: add the matrices
Set the array size to 2 x 2. Select the first cell using the mouse/stylus or the HOME key on your keyboard. Press the "1" button, followed by the "next" button (or the INS key). This enters one into the first cell and moves to the next available cell. Enter "2" then "next" which automatically goes to the next row. Enter 3 and 4 in the same way. The final "next" selects all the cells (remember that if a single cell is selected for the arithmetic operation, it only acts on that one cell). Now click the "+" button (if you are using RPN you will use Enter and "+" at the next step). You enter the second matrix in the same way as the first, "0", "next", "4", "next" and so on. Again click "next" a final time to select all the cells ready for the arithmetic operation. Then click on the "=" button for the result:
Multiplying a matrix by a scalar
A matrix can be multiplied by a scalar very easily by entering the matrix and then making sure all the elements are selected. Now clicking the
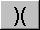 - Matrix product
- Matrix product
The rules for multiplication are more complicated. If we simply use
the multiplication button in the same way as the plus button above we will
carry out a scalar multiplication of the individual cells. Sometimes
we want to do this, but for matrix multiplication we need to use the appropriate
operator which is obtained by clicking the "shift" button, when
the "X" changes to ")(", the matrix multiplication operator.
Example: find the matrix product of the two square matrices
Two matrices may only be multiplied if the number of columns of the first equals the number of rows of the second. If this is the case the matrices are said to be conformable. When we enter non-square matrices we simply ensure that the grid has at least as many rows and columns as the largest matrix. Then we simply leave all the unused elements as zero. The arithmetic deals with conformance, because any non-conforming rows or columns will be multiplied by zero.
(
) (
)
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 5 | 1 | 0 |
| 2 | 3 | 4 | 1 | 3 | 1 |
| 3 | 2 | 0 | 1 | 6 | 2 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
![]() ,
then enter the second matrix..
,
then enter the second matrix..
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 4 | 0 | 0 | 0 |
| 2 | 6 | 2 | 0 | 0 | 0 |
| 3 | 1 | 4 | 0 | 0 | 0 |
| 4 | 3 | 8 | 0 | 0 | 0 |
| 5 | 1 | 7 | 0 | 0 | 0 |
![]()
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 20 | 36 | 0 | 0 | 0 |
| 2 | 35 | 55 | 0 | 0 | 0 |
| 3 | 21 | 74 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
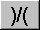 - Matrix division
- Matrix division
For completeness, we have included a matrix division function which is
the equivalent to pre multiplying the numerator matrix by the inverse of
the denominator.
Example: evaluate the following matrix expression
Check:
Note that matrix multiplication is not commutative, so that the order
of multiplication is significant.
Solving a set of linear equations.
The matrix division function gives us an intuitive and easily remembered way of solving a set of linear equations by simply dividing a matrix containing the constants by the coefficient matrix.Example:
Given the set of linear equations:
10x + 2y - 10z =
16 )
-10x + 5y + 12z = 7
)
4x + 6y + 10z
= 36 )
This can be rewritten as a matrix expression:
( 10 2 -10 )
( x ) ( 16 )
( -10 5 12 ) x
( y ) = ( 7 )
( 4 6 10
) ( z )
( 36 )
To solve for (x y z) we do the equivalent of "dividing" both sides by the coefficient matrix, so that:
( x ) ( 16 )
( 10 2 -10
)
( y ) = ( 7 )
/ ( -10 5
12 )
( z ) ( 36
) ( 4
6 10 )
(in reality we will be pre-multiplying by the inverse).
First set the matrix dimensions to 3 x 3 and enter the constants as
a 3 x 1 column matrix (just leave the other elements as zero):
| 1 | 2 | 3 |
| 16 | 0. | 0. |
| 7 | 0. | 0. |
| 36 | 0. | 0. |
Making sure all the cells are selected, we click on the shift
then the divide button (which will be showing ")/(").
Next we enter the coefficient matrix as a 3 x 3 matrix .
| 1 | 2 | 3 |
| 10 | 2 | -10 |
| -10 | 5 | 12 |
| 4 | 6 | 10 |
Finally we press the "=" button to get the resulting values for
x, y and z as another 3 x 1 matrix:
| 1 | 2 | 3 |
| 3 | 0. | 0. |
| 2 | 0. | 0. |
| 1 | 0. | 0. |
which gives us the solution x = 3, y = 2, z = 1.
In practice, it is probably a good idea to enter the coefficient matrix first and save it in memory ready for use, because it is time consuming to enter. You can also use one of the other memories for the constants. This allows you to go back and correct errors without re-entering the whole thing. Be careful when entering negative numbers to use the sign change key "+/-" and not the minus key, which will evaluate the expression using the numbers you entered so far!
Erroneous results can be produced where the set of equations is very "stiff" or has no unique solution, and rounding errors may lead to inaccurate results, if a result is produced at all. In these cases you will need to use more sophisticated numerical techniques than those currently provided by the built-in functions.
 - Transpose
- Transpose
The T button computes the transpose of a matrix. If the matrix
is not square, the largest contained matrix is transposed, while the elements
outside the square are left unchanged.
 - Inverse
- Inverse
Use this button (obtained by shift and the 1/x button) to
invert a matrix. Depending on the values of the elements, it may
not be possible to obtain the inverse, in which case you will get an overflow
error. An example is the inverse of the zero (null) matrix, which
is equivalent to taking the reciprocal of zero in scalar arithmetic.
The inverse can be used as a way of solving a set of linear equations,
although there are more efficient numerical methods. See the matrix
division example above.
 - Determinant
- Determinant
This computes the determinant of a matrix, and is found by using shift
with the "<" (backspace) button. The result is given in
the form of a scalar matrix, i.e. each of the diagonal elements contains
the computed determinant.
 - Unit matrix
- Unit matrix
The unit button generates a unit matrix, i.e. a matrix with zero elements
except for the diagonal elements which are one. It is obtained by
clicking on shift, when the unit button changes to I.
You can use the unit matrix to generate other diagonal matrices.
For example multiply the unit matrix by a constant, or use a simple scalar
multiplication by the unit matrix to obtain the diagonal elements of a
given matrix.
Working with vectors
If the number if I-direction cells is set to exactly 2 or 3 some additional vector functions are available.
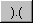 - Scalar Product
- Scalar Product
This button computes the scalar (dot) product of two vectors. The
result is a scalar value, which is represented as its product with the
unit matrix.
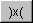 - Vector
Product
- Vector
Product
This button computes the vector (cross) product of two vectors.
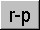 - Rectangular
to Polar
- Rectangular
to Polar
Converts from rectangular (cartesian) to polar coordinates. Use Example: Set number of I cells to 2, J cells to 1. Angle mode is degrees. Enter the value 1.0 into both cells to give the (x, y) coordinates.:
| 1. | 1. |
Now: ![]()
![]() , result:
, result:
| 1.4142135624 | 45. |
The result is in (r, theta) coordinates, where 1.4142... is the square root of 2 and the angle, theta, is 45 degrees.
If the number of I cells is set to 3, the rectangular coordinates are given as (x, y, z) and the result is expressed in cylindrical polar coordinates (r, theta, z).
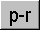 - Polar to Rectangular
- Polar to Rectangular
Converts from polar to rectangular (cartesian) coordinates. Use Sample Problems
Traffic Flow
A proposal for a one-way system is being considered for Matrix Square. The existing traffic flows as shown have already been measured. Assuming no change to the external traffic flows, find the flow of cars per hour through Acacia Street (A), Bond Road (B), Cornish Drive (C) and Durham Avenue (D) given the measured traffic flows in the adjacent roads.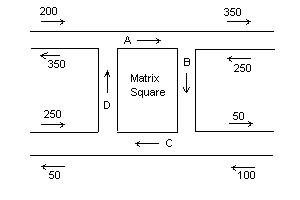
At a first glance it seems insoluble. First, for there to be a solution, the boundary conditions must add up. We can check that the incoming traffic balances the outgoing traffic by noting that 800 cars per hour enter the square, and 800 cars per hour leave it. Good.
Now we need to collect the information we have available. Starting with the junction entering Acacia Street, the net traffic flow per hour consists of 200 cars entering the junction, 350 leaving plus whatever comes through Durham Avenue less the traffic out through Acacia Street, so:
200 - 350 + D - A = 0, or -A + D = 150
Looking at the other junctions in the same way:
A - B = 100
B - C = -50
C - D = -200
In matrix form:
( -1 0 0 1 )
( A ) ( 150
)
( 1 -1 0 0 )
( B ) ( 100
)
( 0 1 -1 0 )
x ( C ) = ( -50
)
( 0 0 1 -1 )
( D ) ( -200 )
To obtain the solution for A, B, C and D we need to enter the constants
as a 4 x 1 column matrix and
| 1 | 2 | 3 | 4 |
| 150. | 0. | 0. | 0. |
| 100. | 0. | 0. | 0. |
| -50. | 0. | 0. | 0. |
| -200. | 0. | 0. | 0. |
then use the matrix divide (")/(" = shift + "/") and then
enter the coefficient matrix.
| 1 | 2 | 3 | 4 |
| -1. | 0. | 0. | 1. |
| 1. | -1. | 0. | 0. |
| 0. | 1. | -1. | 0. |
| 0. | 0. | 1. | -1. |
The result, a 4 x 1 matrix, gives us A = 50, B = -50, C = 0 and D =
200.
| 1 | 2 | 3 | 4 |
| 50. | 0. | 0. | 0. |
| -50. | 0. | 0. | 0. |
| 0. | 0. | 0. | 0. |
| 200. | 0. | 0. | 0. |
Armed with this information, the traffic engineer knows that Durham Avenue needs to handle substantially more traffic than Acacia Street, that Cornish Drive can be pedestrianised, and can alert the police to the 50 cars which will be illegally reversing up Bond Road in any typical hour. The engineer may also wish to review the boundary conditions which are incompletely specified, because an arbitrary amount of circulating traffic can be added while still satisfying the constraints.
You may notice that a large proportion of the elements of this matrix
are zero. This is typical when representing physical problems of
networks or grids of points or control volumes, which result in very sparse
matrices with bands of non zero elements. Another example is given
below.