Complex Numbers
You can carry out complex arithmetic by setting the number of I-direction cells to exactly two, and checking the Complex box in the matrix page of the Options dialog.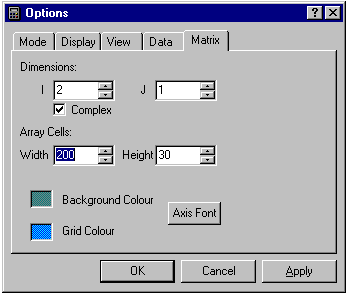
If the number of I-cells is set to some other value you are not allowed to leave the dialog with Complex checked. If you set the number of J-cells greater than one you can work with a one-dimensional array of complex numbers.
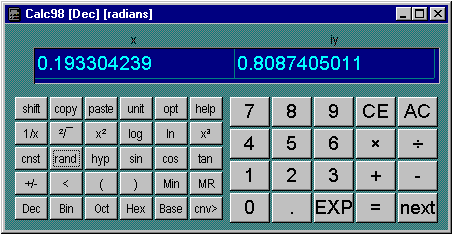
With complex numbers enabled, the column headings in the display are "x" and "iy" to indicate the real and imaginary parts of each number. On a desktop PC, you may want to re-configure the keypads to a landscape layout for complex number arithmetic, because of the extra width needed for the display. You can then adjust the size of the display so that scroll bars are not needed.
You can perform simple arithmetic on complex numbers, or perform exponentiation and logarithm functions and transcendental functions. To enter numbers select the real or imaginary parts as you would array elements as described in the section on arrays and matrices. If you select the real or imaginary part of a complex number, the arithmetic logic acts on the whole of the complex number, not just the part selected.
You can carry out "normal" calculations on real numbers as normal, simply by setting the imaginary part to zero. Of course in certain cases this may give rise to a complex number, for example, famously:
Enter 1, then change its sign ("+/-"). Result:
| x | iy |
| -1. | 0. |
Now take the square root. Result:
| 0. | 1. |
Some examples are given below:
Basic complex arithmetic.
The arithmetic functions act in the same way as for real numbers. Complex addition is the same as array addition, but multiplication and division are slightly more complicated. For example:(x1 + i.y1)(x2 + i.y2) = x1x2 + i.x1y2 + i.x2y1 + i 2.y1y2
= (x1x2 -y1y2) + i.(x1y2 + x2y1)
Complex plane.
To convert from real and imaginary components to modulus and argument in the complex plane (Argand diagram), use the normal r-p and p-r buttons. These are obtained by using the shift key when they replace the "+" and "-" arithmetic buttons. Once converted, the calculator does not "know" the values are in polar co-ordinates, and you must convert back to cartesian form to continue calculations. The argument will be expressed in degrees, radians or gradients depending on the angle mode selected.Example:
Visualizing complex numbers in the complex plane is a powerful way of thinking about the real and imaginary components of numbers. The behaviour of arithmetic operations can be grasped more easily by considering the geometric equivalents in the complex plane. For example, to take the square root of a complex number, take the square root of the modulus and divide the argument by two. You can verify this by using the calculator to take the square root of various numbers and converting them to polar co-ordinates.