Financial Functions
To select the financial functions, press 
and select Financial mode from the Mode tab, or use shift then the 
button. The title bar ends with [fin] when you are in financial
mode. You can also use the Display tab to select commas to separate
thousands. In Financial mode, numbers are always displayed with a fixed
point and two decimal places.
In financial mode, some of the scientific functions are replaced by the financial functions. These fall into two groups: those concerned with calculating compound interest on loans, and those used for budgeting.
- Set Interest
and Discount Rates
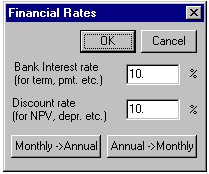
The bank interest rate is applied to the loan calculations (
,
,
and 
) and
the discount rate to the Net Present Value calculations (
and 
). Typically
these will be assigned different values which prevail at the time and in
the relevant field of commerce.
It is assumed that the period in these calculations is one year. If a different period is required (monthly for example), then the rates should be adjusted to their equivalent monthly rates. To make this easier, there are two buttons marked Annual->Monthly and Monthly->Annual. Typically, you would enter an annual interest rate in the two boxes, and then click on the Annual->Monthly button to convert to the equivalent monthly rate (by dividing by 12). You can convert back to annual using the Monthly->Annual button. Each click divides or multiplies the rate by 12.
Other periods can also be used, but you will need to enter the appropriate rate for the time period. Often the rate is known for some other period and the required rate will need to be calculated. This can be done by using the calculator and cutting and pasting. Be careful to select decimal mode to compute interest rates before copying, because the financial mode will truncate the result to two decimal places which may not be sufficiently accurate.
- Calculate
term of investment
To compute the term required for an investment to increase to a given value,
enter the principal, followed by
followed by the desired compounded sum at the term. The result is the number
of periods (generally years) required for the investment to reach this
value. If you wish to use a different period (monthly for example) you
need to change the value of the interest rate accordingly, by pressing .
Example:
How many years of compound interest are required for an initial investment
of $100 to reach the value of $200 (assuming 10% bank interest rate)?
1 0 0 2 0 0 
Result: 7.27 (i.e. 8 years to exceed $200).
- Calculate Value
of Annuity
To calculate the value of an annuity at maturity, enter the amount of the
annual payment, then ,
followed by the number of years.
Despite the literal meaning of the word annuity, it is possible to use
a period other than annual in the calculation, in which case you need to
change the value of the interest rate accordingly, by pressing .
Example:
What is the value at maturity of a 30 year annuity with an annual payment
of $200 (assuming an interest rate of 10%)?
2 0 0
3 0
Result: $32898.80
- Calculate
Mortgage payment
To compute the required periodic payments to repay a given loan, enter
the amount of the loan, click the
button, then enter the duration (number of payments). Press = to
get the amount of each payment. Usually the term of a mortgage is
defined in years, but the repayment periods and corresponding calculations
are carried out monthly.
Example:
What is the monthly payment to pay off a loan of $30,000 dollars over
25 years at an interest rate of 10% ?
First click on
to check that the interest rate is set to 10% (and change it if needed),
and click on Annual->Monthly. The interest rate displayed
changes to 0.83333...%.
The period is now in months, which over 25 years is 25x12 months (i.e. 300 months).
3 0 0 0 0 
2 5 
12
Result: $272.61 (the monthly payment)
- Calculate Value
of an Investment
To compute the value of an investment after a given number of years at
the current interest rate, enter the principal, click Inv and the
number of investment periods. Usually the number of periods is the number
of years. If you wish to use a different period (monthly for example) you
need to change the value of the interest rate accordingly, by pressing.
Example:
What is the value of $100 invested for five years at compound interest
(assuming a 10% annual interest rate)?
1 0 0
5
Result: $161.05
- Calculate Net
Present Value of a Future Cash Flow
To calculate the present value of an amount to be paid at some time in
the future, enter the value of the amount, followed by
and then the number of periods before the payment will be made. Usually
the number of periods is the number of years. If you wish to use a different
period (monthly for example) you need to change the value of the discount
rate accordingly, by pressing .
You can enter a negative number of periods, in which case you get the
present value of a payment which was paid at some time in the past. If
you require the net present value of a series of periodic cash flows, use.
Example:
What is the net present value of $100 to be paid in five years time
(assuming 5% discount rate).
1 0 0 5
Result: $78.35
... - Net Present Value of Cash Flows
To calculate the net present value of a series of cash flows, enter the
cash flow for each period followed by the
button. Each time this button is pressed, the button legend is incremented
indicating the next periodic cash flow to be input, e.g. after the first
period is input the button shows .
At any time you can display the cumulative net present value of the cash
flows input so far by pressing =. To reset the period back to 1
and erase the accumulated values press the
AC button.
Typically the period is annual. If you wish to use a different period
(monthly for example) you need to change the value of the discount rate
accordingly, by pressing .
It is also permitted to alter the discount rate during the calculation
(i.e. rate differs for different periods). If you require the net present
value of a single cash flow at some point in the future, use the
button instead.
Example:
A project requires an initial capital expenditure of $1,000,000. After
five years the capital equipment is to be written off. The expected annual
revenue stream, less running costs, is: year 1 - $100,000; year 2 - $200,000,
year 3 - $300,000, year 4 - $300,000, year 5 - $300,000. The net revenues
exceed the initial capital cost, but is the investment a good one, assuming
a discounting rate of 5% per annum?
1 0 0 0 0 0
2 0 0 0 0 0
3 0 0 0 0 0
(Intermediate result: $535795.27 in display)
3 0 0 0 0 0 
3 0 0 0 0 0 
Result: $1017663.86
The result shows that, taking into account the time value of money, the revenue flows have a net present value of $1017663.86, so that the project is just profitable (but probably not worth the risk!).
- Straight Line
Depreciation
To calculate the fraction of the value of an asset which is depreciated
after a given time using straight-line depreciation, enter the initial
cost less any salvage value, then ,
followed by the useful asset life, then
, followed by the number of periods after which the depreciation is to
be calculated, followed by =. The result is the total (cumulative)
depreciation charge.
Usually the number of periods is the number of years. If you wish to
use a different period (monthly for example) you need to change the value
of the discount rate accordingly, by pressing .
Example:
What is the depreciation after five years on a capital asset costing
$10,000 with a ten year life and a salvage value of $1000 at the end of
its life?
1 0 0 0 0 
1
0 0 0
Result: $9000.00
1 0 5
Result: $4500.00
The depreciation is $4500, therefore the value of the asset after 5 years is $10000 - $4500 = $5500.00
- Double declining
Balance Depreciation
To calculate the fraction of the value of an asset which is depreciated
after a given time using the double-declining balance method of depreciation,
enter the initial cost less any salvage value, then ,
followed by the useful asset life, then ,
followed by the number of periods after which the depreciation is to be
calculated, followed by =. The result is the total (cumulative)
depreciation charge.
Usually the number of periods is the number of years. If you wish to
use a different period (monthly for example) you need to change the value
of the discount rate accordingly, by pressing .
Example:
What is the depreciation after five years on a capital asset costing
$10,000 with a ten year life and a salvage value of $1000 at the end of
its life?
1 0 0 0 0 1
0 0 0
Result: $9000.00
1 0 5
Result: $6030.00
The depreciation is $6030, therefore the value of the asset after 5 years is $10000 - $6030 = $3970.00
- Sum-of-Years-Digits
Depreciation
To calculate the fraction of the value of an asset which is depreciated
after a given time using the sum-of-years-digits method of depreciation,
enter the initial cost less any salvage value, then ,
followed by the useful asset life, then ,
followed by the number of periods after which the depreciation is to be
calculated, followed by =. The result is the total (cumulative)
depreciation charge.
Usually the number of periods is the number of years. If you wish to
use a different period (monthly for example) you need to change the value
of the discount rate accordingly, by pressing .
Example:
What is the depreciation after five years on a capital asset costing
$10,000 with a ten year life and a salvage value of $1000 at the end of
its life?
1 0 0 0 0 1
0 0 0
Result: $9000.00
1 0 5
Result: $6570.00
The depreciation is $6570, therefore the value of the asset after 5 years is $10000 - $6570 = $3430.00